Adaptation has a diversity of meanings, even within areas in which it is widely used, such as anthropology, biology, the humanities, and in common parlance. The study of adaptations is a central activity in biology, where interpretations of the concept have received much scrutiny in recent years, for example, in the articles and monographs of Andrews, Brandon, Gould and Lewontin, Gould and Vrba, Rose and Lauder, Sober, and Williams. Gould and Verba pointed out the presence of two distinct adaptation concepts in the literature: one historical, emphasizing traits’ origins and their past histories of selection, the other nonhistorical, emphasizing current functions of traits and their contributions to fitness. For example, some argue that to be regarded as an adaptation, a trait must have been produced by natural selection, and so must be genetically inherited. Gould and Lewontin distinguished adaptations from exaptions. The latter are preexisting traits that at some time in the past acquired beneficial effects without being selected for them at that time. However, exaptions may subsequently be modified by natural selection as a result of their new functions. The concept of exaptions seems to have little relevance to studies of extant species. A meaning common in physiology and the social sciences is that an adaptation is a beneficial modification of an organism that adjusts it to changes in the environment. In many cases, these changes are homeostatic. For example, changes in the size of the pupil keep the light intensity at the retina within the optimal range for vision. If effects of such phenotypic adjustments lead to increased survival and reproductive success, that is, to greater fitness, they and the machinery of the body (nerves, muscles, and so on) that produce them are adaptations in the core sense described below.
Another common requirement for a trait to be considered adaptive is that its functional consequences must be consistent with a priori design specifications for accomplishing a specified task. For example, in order to transport oxygen from the lungs to the rest of the body, blood must include a component that binds to oxygen in the lungs yet subsequently releases it in tissues that are oxygen depleted. Hemoglobin has exactly this property, as revealed by its oxygen dissociation curve. Optimality models used in behavioral are comparable to the engineering specifications used in functional anatomy. Both attempt to identify characteristics of functional designs for specific tasks. At the heart of the use of design specifications is the question: Under existing circumstances, how would a well-adapted organism of this species behave or be structured? Design specifications play an important role in the study of adaptations, at every level of biological organization. At the core of these diverse interpretations is the idea that adaptations are traits that benefit the organism. In many cases, these benefits result from effects on vital processes, such as maintaining osmotic balance, obtaining food, avoiding predators, caring for offspring, and so forth. The ultimate criterion of benefit is that a trait’s effects must be functional, in the sense of enhancing fitness. In some cases, adaptation refers to the processes that select for such traits. Adaptations may be at any level of organization: biochemical, physiological, anatomical, or behavioral.
Measuring Adaptiveness in Extant Species
From the standpoint of the current functions of traits and their impact on fitness, a trait variant is better adapted, relative to competing variants in other individuals of the same species, to the extent that it directly augments fitness. Thus, in studies of living organisms, one can confirm that a trait is adaptive and measure its degree of adaptiveness by determining its effect on fitness. However, just confirming that traits are adaptive leaves unanswered some of the most interesting questions about a trait, such as: What correlated traits augment fitness because they affect the same vital functions, and what are their relative contributions? By what means does a trait augment fitness, and how strongly is it being selected? Adaptation requires a mechanism.
Following is an abbreviated description of several research approaches that, depending on one’s choice among them, can answer the questions above, providing quantitative measures of the relative adaptiveness of traits in terms of their contributions to functions as well as fitness. They enable one to evaluate the direct force of characters on fitness, excluding effects from correlated traits. They are based on phenotypic selection but not the genetic response to selection; thus, they require only data that can be obtained within a single generation and require no assumptions about the genetic basis or evolutionary history of the traits. They take advantage of individual differences in traits in a local population of a species and are applicable to polygenic traits, such as those commonly studied by anthropologists, evolutionary psychologists, and biologists. Some are based on a priori design specifications of optimal phenotypes, others on multivariate selection theory, especially the work of Russell Lande and Stevan Arnold, which deals with the effects of selection acting simultaneously on multiple characters.
Components
Depending on the choice of approach, various combinations of the following four empirical components are used: (a) samples, taken in a local population of a species, of individual variants in a set of phenotypic traits known or thought to affect a specified vital activity, such as getting food or obtaining mates; (b) samples of proximate effects (“performances”) of these variants, whether functional or otherwise; (c) a quantitative optimality model of one or a combination of traits and corresponding proximate effects that are posited to augment biological fitness; and (d) estimates of lifetime fitness of each individual.
The approaches will be illustrated by a fictitious study of fishing success of women in a local population. They spearfish independently in the nearby lakes. The fish that a woman catches are eaten only by her family and are the primary staple of their diet. The only exceptions are fish exchanged in barter for other goods. Three traits of the women affect their relative fishing styles and are measured. Women with the best visual acuity favor lake edge shallows, where only they can see the small fish hiding among the water plants. Only the tallest women fish regularly in deep water, where fish are largest, oldest, and relatively slow moving, but scarce. Women with the greatest competence with a spear tend to fish in water of intermediate depth, where they have a unique ability to catch the fast-moving, mature fish.
Two aspects of the women’s daily catch seem to be of particular importance: their success at catching pescos, a rare and highly prized fish, very valuable in barter, and the total mass of other fish that they catch. Each day, the weight of pescos caught by each female and the weight of the rest of her catch are recorded. Seasonal totals of these two sets of values for each female provide two measures of her fishing success.
First approach: Evaluate the causal link from any selected trait to fitness. To measure the potential impact on relative fitness of each phenotypic trait, regress relative fitness w on it.However, because fitnessaffecting traits may be correlated, use partial regression βwzi (ordinary, not standardized) to measure the direct impact of the ith trait, zi, on relative fitness w, with indirect effects from correlated traits thus held constant. Repeat for each of the other traits that may affect relative fitness. Then, to document any correlations among these traits, calculate their covariances (unstandardized correlations).
Relative fitness w of an individual is defined with respect to the mean fitness in the population, w = W/W — , where Wis the absolute fitness of an individual and W — is the mean fitness in the population. The fitness of individuals can be estimated in several ways, particularly by using aspects of reproductive success, such as the number of surviving offspring. Individual fitness can be measured at long-term study sites of populations on which basic demographic data are consistently recorded and maintained; for data sets of shorter duration, it can be estimated from various components of fitness. The partial regression of relative fitness on a given character is its selection gradient. It measures the change in relative fitness expected if that character were changed by a unit amount but none of the other characters varied. A remarkable result, due to Russell Lande, is that for a set of characters that affect fitness, including all phenotypically correlated traits that directly affect fitness, their selection gradients, arranged as a vector, include all the information about phenotypic selection (but not inheritance) that is needed to predict the directional response to selection.
So, in the case of our study of fisherwomen, we would regress their relative fitness on their visual acuity (ability to see fish hiding in the shallows), on their height (deep-water fishing ability), and on their spearing competence, then calculate the three covariances among these three traits.
Second approach: Evaluate the causal link from each trait to its proximate effects, then the link from each proximate effect to fitness. The first approach, above, evaluates the causal links from traits to fitness by determining their selection gradients. However, that approach does not tell us anything about the intervening functional effects of traits that augment fitness. In 1983, Stevan Arnold used Sewall Wright’s method of path analysis to provide a convenient means of partitioning selection gradients (see Figure 1). He showed that for any character zi (such as z1 in Figure 1) that affects only one performance variable fj, a selection gradient βwzi can be partitioned into two parts: a performance gradient βfjzi , representing the effect of the trait on some aspect of performance, and a fitness gradient βwfj, representing the effect of performance of fitness. That is,
Βwzi = βfjzi • βwfj
Selection performance fitness
gradient gradient gradient
where βwfj is the partial regression of relative fitness w on the performance variable and βfjzi is the partial regression of the performance variable on its trait variable.
A trait may affect more than one performance variable, resulting in branching paths. For example, the second trait z2 in Figure 1 affects two performance variables, f1 and f2. In that case, the total path connecting character z2 with relative fitness is the sum of the two paths, one through effect variable f1 and one through effect variable f2, as shown in Figure 1. The corresponding relationship in partial regression coefficients is βwz2 = βf1z2 βwf1 + βf2z2 βwf2. Thus, the total selection gradient can be partitioned into parts, corresponding to branching paths of influence on fitness, as well as factored along paths. These elementary results can be expanded for analysis of selection gradients in situations considerably more complicated than that of the fictitious fisherwomen depicted in Figure 1.
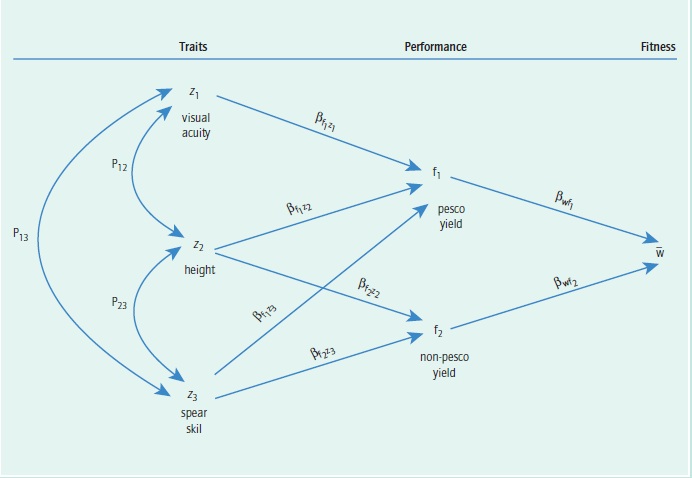
Figure 1. Effects of each phenotypic trait (z terms), such as visual acuity, height, and spear skill in fisherwomen, on performance (f terms), such as yields of pesco and non-pesco fish, and then the effects of performance variables on biological fitness (w term). P terms on double-headed arrows represent covariances among traits, and ß terms represent partial correlations, as described in text.
Of course, we want to know the magnitude of the influence of various traits on a given proximate effect, not just whether they can have any influence. For this purpose, we use each trait’s performance gradient to calculate that trait’s average contribution to the mean value of a given effect.
Third approach: For a selected vital task, devise and test an optimality model. Such a model would be based on optimizing (maximizing or minimizing, as appropriate) a performance variable presumed to have a major net impact on fitness, taking into account the variable’s benefits and also correlated costs and entailed constraints.
The benefit variable to be optimized is represented by an objective function. If the detrimental effects of some cost variables change continually as the benefit variable changes, the cost and benefit variables can be combined into a single cost-benefit function, to be optimized. For cost variables that exhibit their detrimental effects only when they exceed a threshold value, those values are each represented by an appropriate constraint function. Those diets that meet all constraints are adequate: They meet minimum requirements for all nutrients without exceeding any limits on toxins or other hazards.
For our hypothetical fisherwomen, their fishing is a contribution to the vital task of getting enough food and the right kinds. Suppose that during a period when catches are poor, their protein intakes and those of their families are so low that increases in protein intakes are expected to result in greater increases in survival and reproductive success than would a change in any other attribute of their diets. Then, their objective would be to increase their protein intake, which for them comes almost entirely from fish.
In a protein maximization model for their fishing, this objective is made explicit by an objective function. Suppose that pesco fish are 17% protein and all other fish are 12% protein. Then, the weight of protein P in a woman’s catch on a given day can be calculated from the linear function P = 0.17f1 + 0.12f2, where f1 is the weight of her pesco catch that day and f2 is the weight that day of her catch of other fish. In a simple model, the objective could be to maximize P. Suppose, however, that greater time devoted to fishing results in progressively less time available for other vital activities, and thus in decrements in fitness. In that case, the objective function would be for a net effect, chosen to reflect this cost-benefit trade-off.
A variety of constraints would further limit a woman’s ability to obtain more protein. She cannot maximize protein by limiting her catch to the protein-rich pescos, because they are rarely caught. Other constraints that might restrict her protein yield include maximum effort that she can devote to fishing and the need to remain below her maxima for all toxins or other hazards entailed by consuming any given diet. For example, if pesco fish are unusually rich in vitamin D, the upper limit on safe vitamin D intake establishes a maximum daily safe consumption of pesco, even though they are very rich in protein. If the largest non-pesco fish occur only in the cold, deep water, the dangers of hypothermia and drowning might place an upper limit on the time that can safely be devoted to those fish. The success of an optimality model depends on one’s ability to incorporate as much relevant natural history as possible into the choice of the objective function and its constraints.
In addition to the optimality model itself, three forms of data are required for this approach. They are the same as in the second approach, namely, (a) individual values of phenotypic traits that are relevant to the model (in our example, values for the three traits that contribute to successful fishing and for each constraint-related trait); (b) proximate effects (the weight of each female’s pesco and non-pesco catch and their respective protein concentrations); and (c) fitness (how long each subject survived and her lifetime reproductive success).
A model is basically an elaborate hypothesis, for which the common method of confirmation is a goodness-of-fit test. For an optimality model, such a test would tell us whether the individuals or their mean were at or near the specified optimum. However, for a host of reasons, reviewed by Altmann, Dawkins, Rose and Lauder, and also Emlen, most organisms are unlikely to be performing at or near optimum. For example, the constraint set may not be complete, and so the putative optimum may be beyond reach. A more reasonable question to ask is whether those individuals that are closer to the optimum specified by the model have higher fitness, as in Altmann’s study of foraging in yearling baboons (see Figure 2).
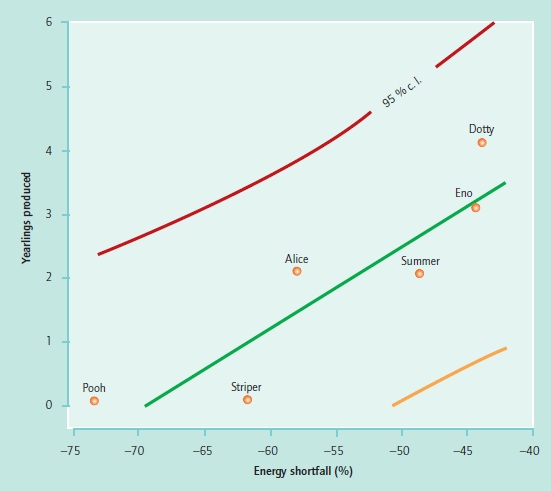
Figure 2 Reproductive success of female baboons (number of surviving yearlings that they each produced in their lifetime) as a function of their energy shortfalls as yearlings (percent deviation of their actual intakes from their respective optimal intakes). Adjusted R2 = 0.76, p = 0.05.
Confirming an optimality model in this way is, at the same time, a confirmation of adaptive differences in the specified traits and in our identification of the functional mechanisms by which these traits affect fitness.
Thus, if, up to a point, women whose catches yielded more protein have higher fitness than other women—if the objective function of the model is, as had been assumed, a limiting factor for fitness—her fishing and the constellation of traits involved in it are more adaptive than those of the other women.
Fourth approach: Evaluate the causal links from each trait to its proximate effects. What can we do to evaluate adaptiveness if data on fitness are not (yet) available? Method 2 was based on Arnold’s separation of fitness into two parts: a performance gradient representing the effect of the trait on some aspect of performance and a fitness gradient representing the effect of performance on fitness. We can take advantage of the ability of performance gradients to isolate the effect that each trait has on a given performance from effects of correlated traits, and we can quantitatively evaluate the contribution made by each trait to each performance variable. If we assume that through their impact on vital processes, each of these performance variables affects fitness, they are indicative of the adaptiveness of the traits, even though in the absence of fitness data, we would be unable to test that assumption.
If we had an optimality model (third approach), we would already have hypothesized how to combine trait variables into quantitative predictions of each individual’s level of performance on the most fitness-enhancing performance variable, and thus to predict its fitness.
Recent developments in interspecific comparative methodology, involving phylogenetic analysis of homologous traits, provide another approach to documenting that a trait is an adaptation and studying the evolution of correlated traits. For the study of living humans, however, the lack of any surviving species of the same genus or even family greatly limits the applicability of these methods in cultural anthropology. Similarly, alteration or removal of traits, though sometimes used in experimental biology to study the functions of traits, would be unacceptable in studies of living humans, except perhaps where such changes are made independently, for cultural or medical reasons. (Do I chew differently without my third molars?)
Fifth approach: Evaluate the adaptiveness of a trait by whether its effects are beneficial by intuitively reasonable criteria. Suppose that we have neither the data to evaluate performance gradients or selection gradients nor a model of optimal phenotype. What then? One possibility is to use our knowledge of the subjects’ needs or deficiencies, particularly ones having major effects on survival or reproduction, and our evaluation of the efficacy of various traits to satisfy these needs. This basic technique has enabled medical research to uncover hundreds of functional traits, without recourse to measures of fitness or heritability.
If members of our local fishers’ families show signs of protein malnutrition, then even before the first of them has died from it, we can reasonably assert that those fishers who bring home a larger harvest of fish have adaptive fishing practices. On the other hand, if the local human population shows signs of scurvy, then the woman who brings back a bounteous catch of fish only because she fished longer has traits that are less adaptive than the one who fished just long enough to satisfy her family’s protein requirement, then went off in search of fruit—which, she has noticed, alleviates the symptoms of scurvy.
For centuries, descriptive naturalists have identified a wide variety of adaptations. Charles Darwin described dozens of them. Although the criteria that descriptive naturalists use to identify adaptations seem never to be made explicit, their descriptions indicate that they rely on noticing uses to which physical traits and behaviors are put, particularly exaggerated ones, and especially in comparison with corresponding traits in related species. These methods of observant physicians and naturalists are no less valid today, even if they have neither the scope of some methods described above nor the ability of those methods to systematically disentangle and measure complex interrelationships.
References:
- Altmann, S. A. (1998). Foraging for survival: Yearling baboons in Africa. Chicago: University of Chicago Press.
- Arnold, S. J. (1983).Morphology, performance, and fitness. American Zoologist, 23, 347–361.
- Cronk, L., Chagnon, N., & Irons,W. (Eds.). (2000). Adaptation and human behavior: An anthropological perspective. New York: Aldine de Gruyter.
- Hill, K., & Hurtado, A. M. (1996). Ache life history: The ecology and demography of a foraging people. New York: Aldine de Gruyter.
- Lande, R., & Arnold, S. J. (1983). The measurement of selection on correlated characters. Evolution 37, 1210–1226.
- Rose, M. R., & Lauder, G. A. (Eds.). (1996). New York: Academic Press.
- Smith, E. A.,Mulder, M. B., & Hill, K. (2001). Controversies in the evolutionary social sciences: A guide for the perplexed. Trends in Ecology and Evolution, 16, 128–135.
- Sober, E. (1984). The nature of selection. Cambridge: MIT Press.
- Williams, G. C. (1966). Adaptation and natural selection. Princeton, NJ: Princeton University.
